Neural PDE
Regularizing Image Classification with Partial Differential Equations [PDF]
Joining BigDyl Laboratory
Joining the big data analytics lab of Yonsei University and starting my research internship under the supervision of Prof. Noseong Park, was in fact the beginning of proper research journey. Though I had experience in Application Platform Lab as a research intern, at the time I focused mainly on code development and conducting experiment to improve performance, not research nor writing papers. As I joined the BigDyl lab, I started working on this project, so called Partial Differential Equation Regularized Neural Net (PR-Net). This was a project which my brother Seunghyun Hwang, who is currently a Ph.D. student in Purdue University in electrical engineering, and at the time who was also a student in Yonsei University computer science department, suggested me to collaborate with. Discussing Neural ODE and physics informed neural network (PINN), I was deeply intrigued by this subject.
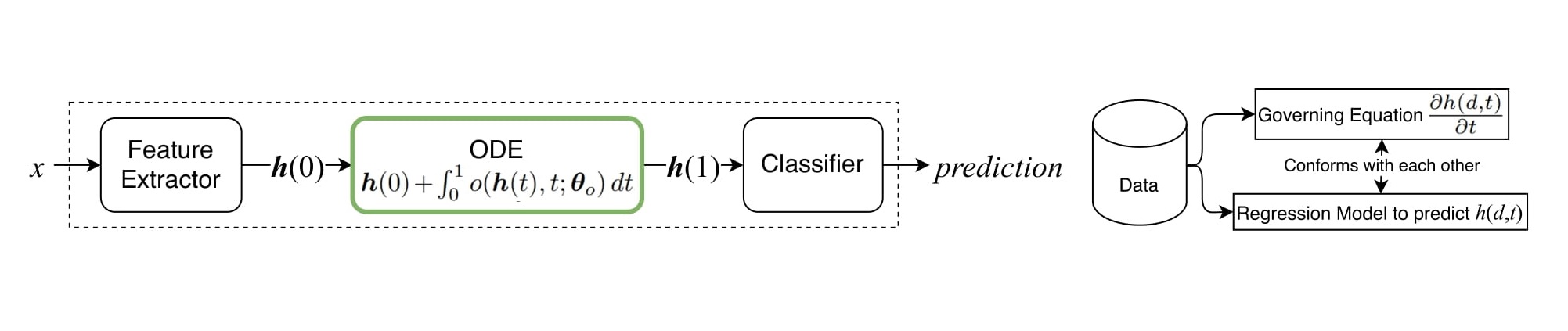
Concept of PR-Net
Our proposed method, however, propose the concept of partial differential equation-regularized neural network (PR-Net), to directly learn a hidden element, denoted h(d,t) at layer (or time) t